Understanding the grid structure • hexmap

library(hexmap)
library(sf)
library(ggplot2)

Consider a map with boundaries $(x_1, y_1, x_2, y_2)$ such that

$x_1$ and $x_2$ denote the minimum and maximum longitude of the map, respectively,
$y_1$ and $y_2$ denote the minimum and maximum latitude of the map, respectively,
$A = (y_2 - y_1)(x_2 - x_1)$ is the total area of the map,
$L$ is the total land area of the map,
$n_{xe}$ and $n_{xo}$ is the total number of hexagons on even and odd rows respectively,
$n_{ye}$ and $n_{yo}$ is the total number of hexagons on even and odd columns respectively,
$n_r$ and $n_c$ are the maximum number of rows and columns in the grid structure,
$n$ is the desired total number of hexagons,
$c$ is the cell size, which is the same as the width of the non-flat topped hexagon.

We assume that the hexagon is not flat topped. Note that $A$ , $L$ , $n$ , $x_1$ , $x_2$ , $y_1$ and $y_2$ are known.

Below is an example where the “map” is a unit square. In this case $A = L$ .

square <- matrix(c(0, 0, 
                   0, 1, 
                   1, 1, 
                   1, 0, 
                   0, 0), 
                 ncol = 2, 
                 byrow = TRUE) %>% 
  list() %>% 
  st_polygon()

plot_hex_tile <- function(cellsize = NULL, n = NULL) {
  title <- ifelse(is.null(cellsize),
                  paste0("n = ", n),
                  paste0("Cell size = ", cellsize))
  if(is.null(cellsize)) {
    title <- paste0("n = ", n)
    grid <- st_make_grid(square, n = n, square = FALSE)
  } else {
    title <- paste0("Cell size = ", cellsize)
    grid <- st_make_grid(square, 
                         cellsize = cellsize,
                         square = FALSE)
  }
  
  ggplot(grid) +
    geom_sf(fill = "transparent") + 
    geom_sf(data = square, fill = "transparent", color = "red") +
    ggtitle(title)
}

plot_hex_tile(0.25)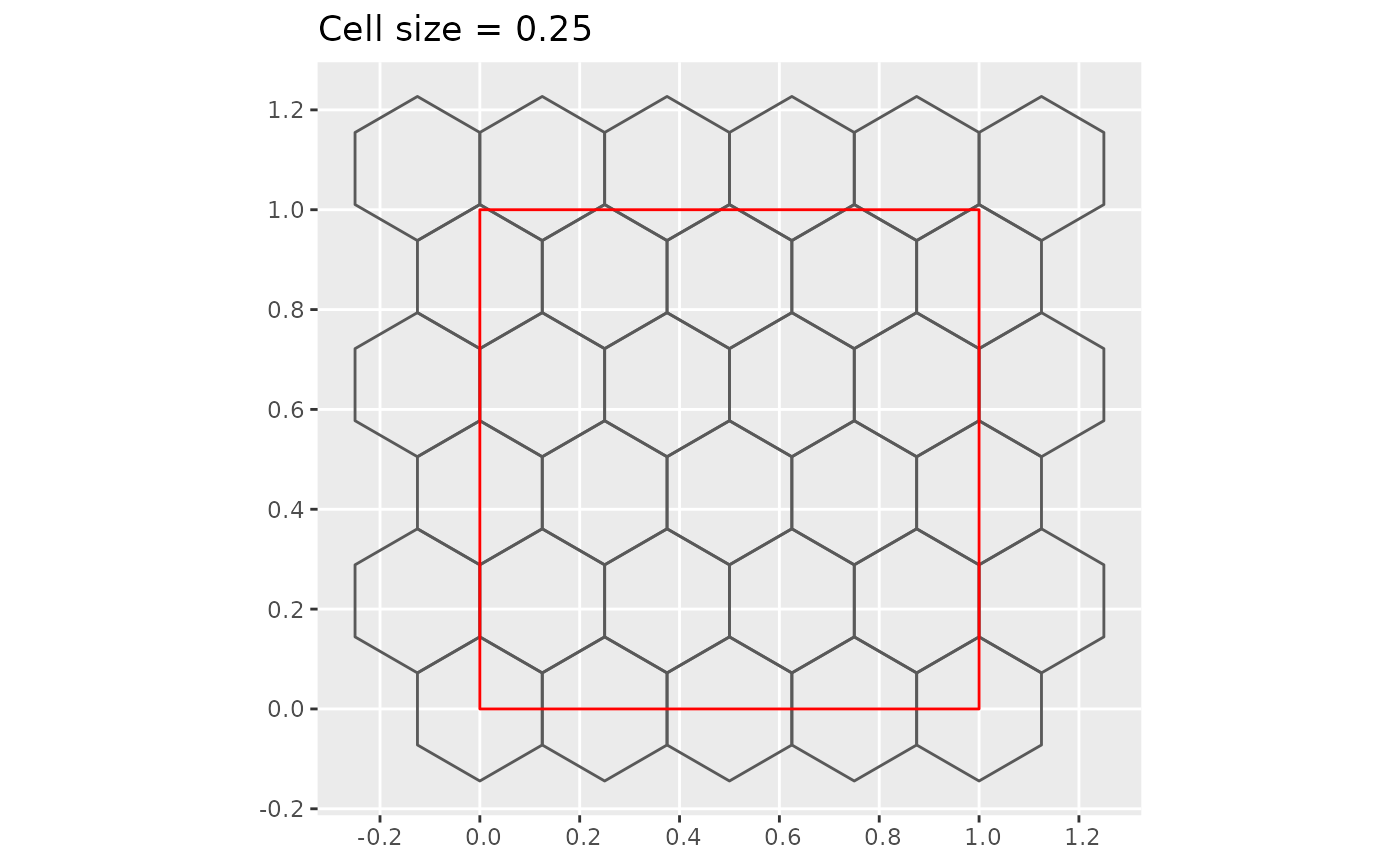

plot_hex_tile(0.3)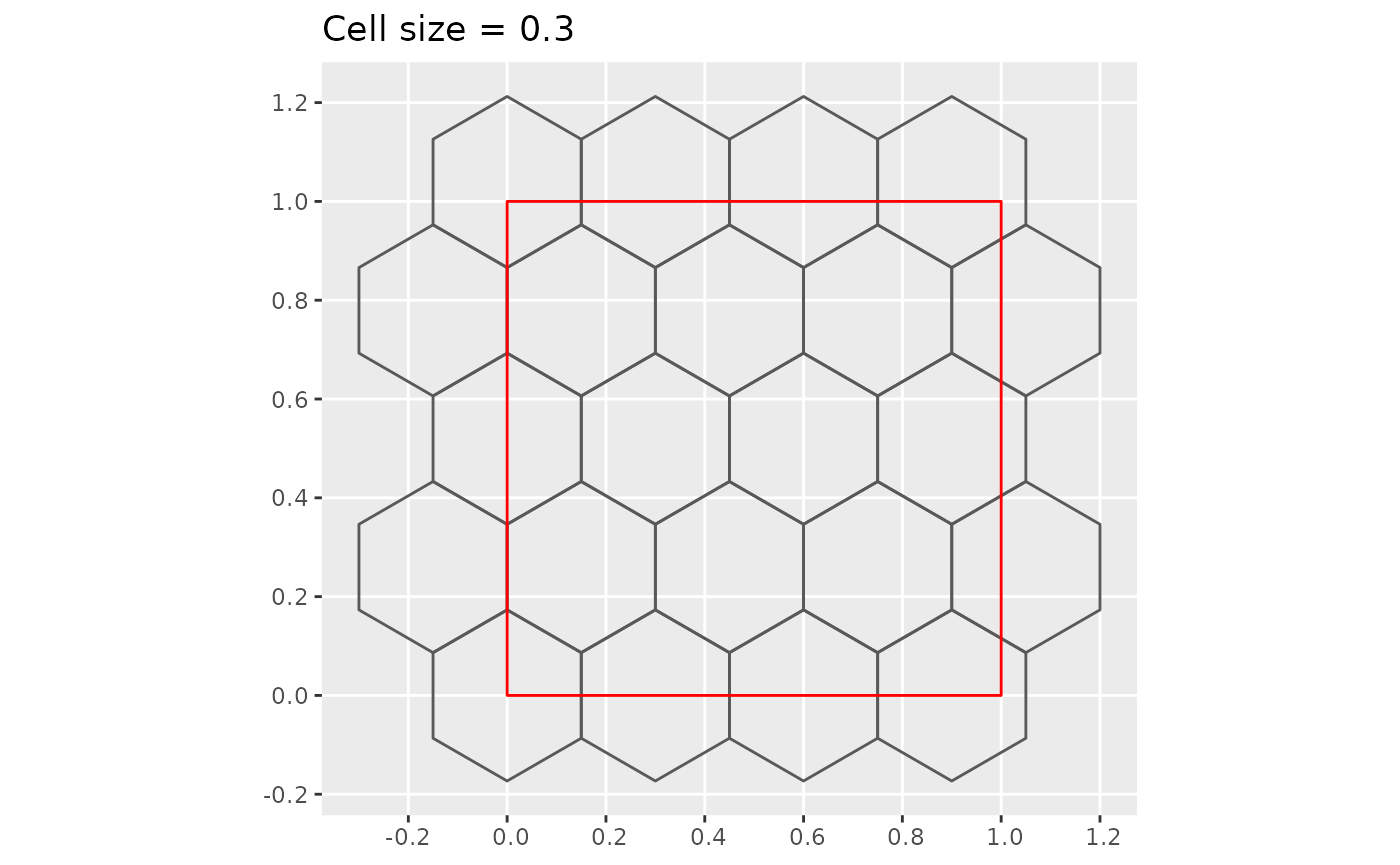

plot_hex_tile(0.5)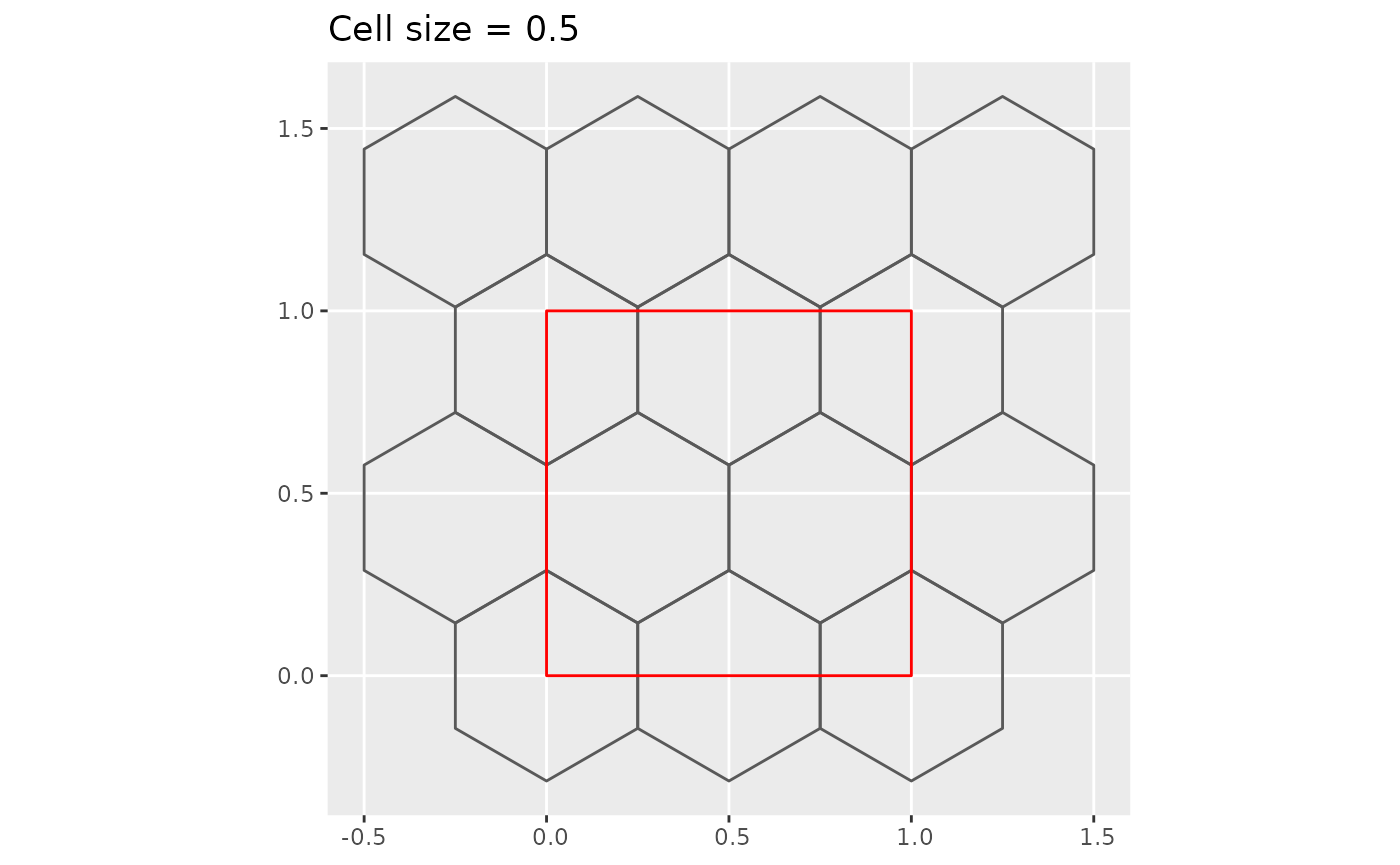

plot_hex_tile(1)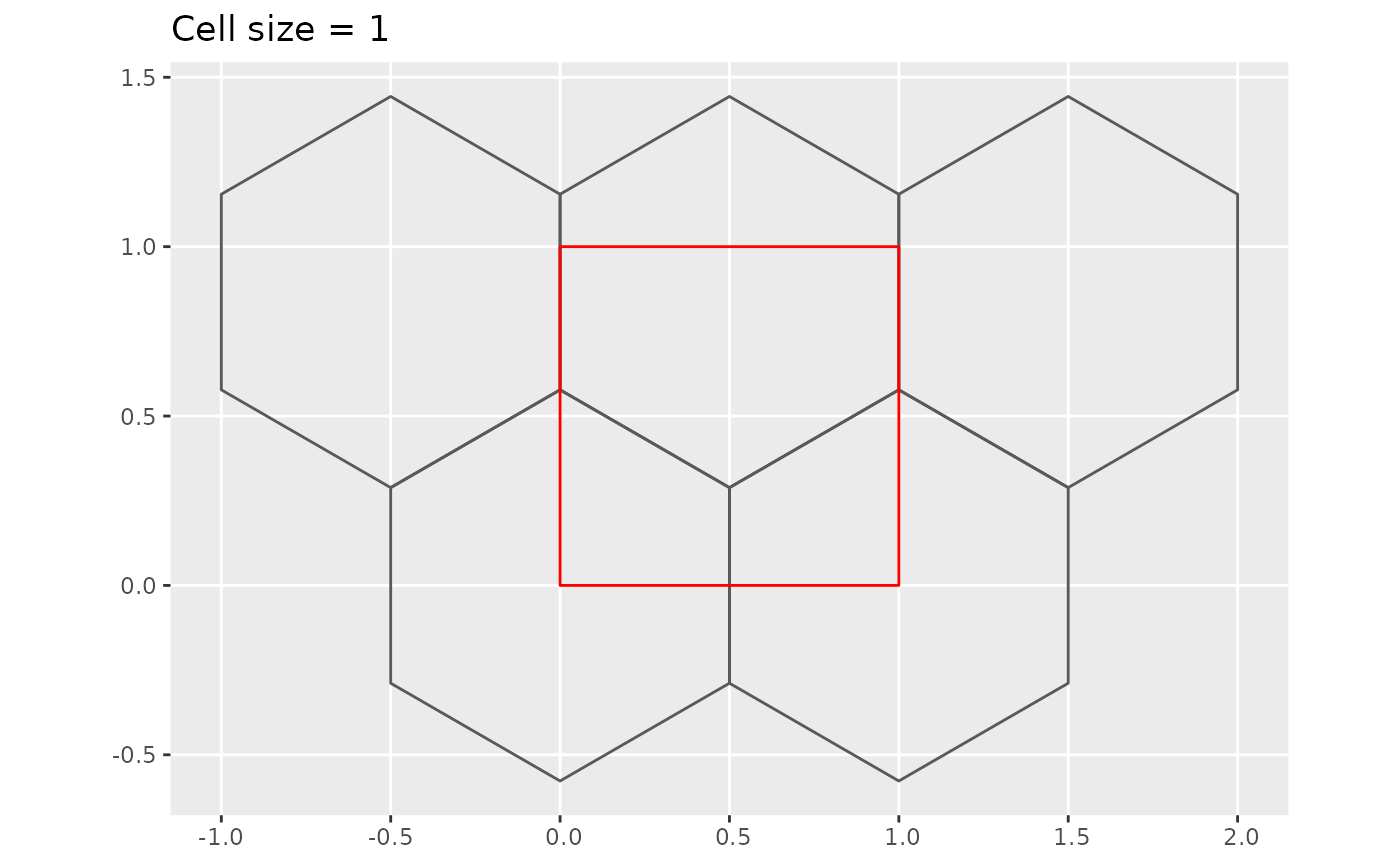

plot_hex_tile(n = 3)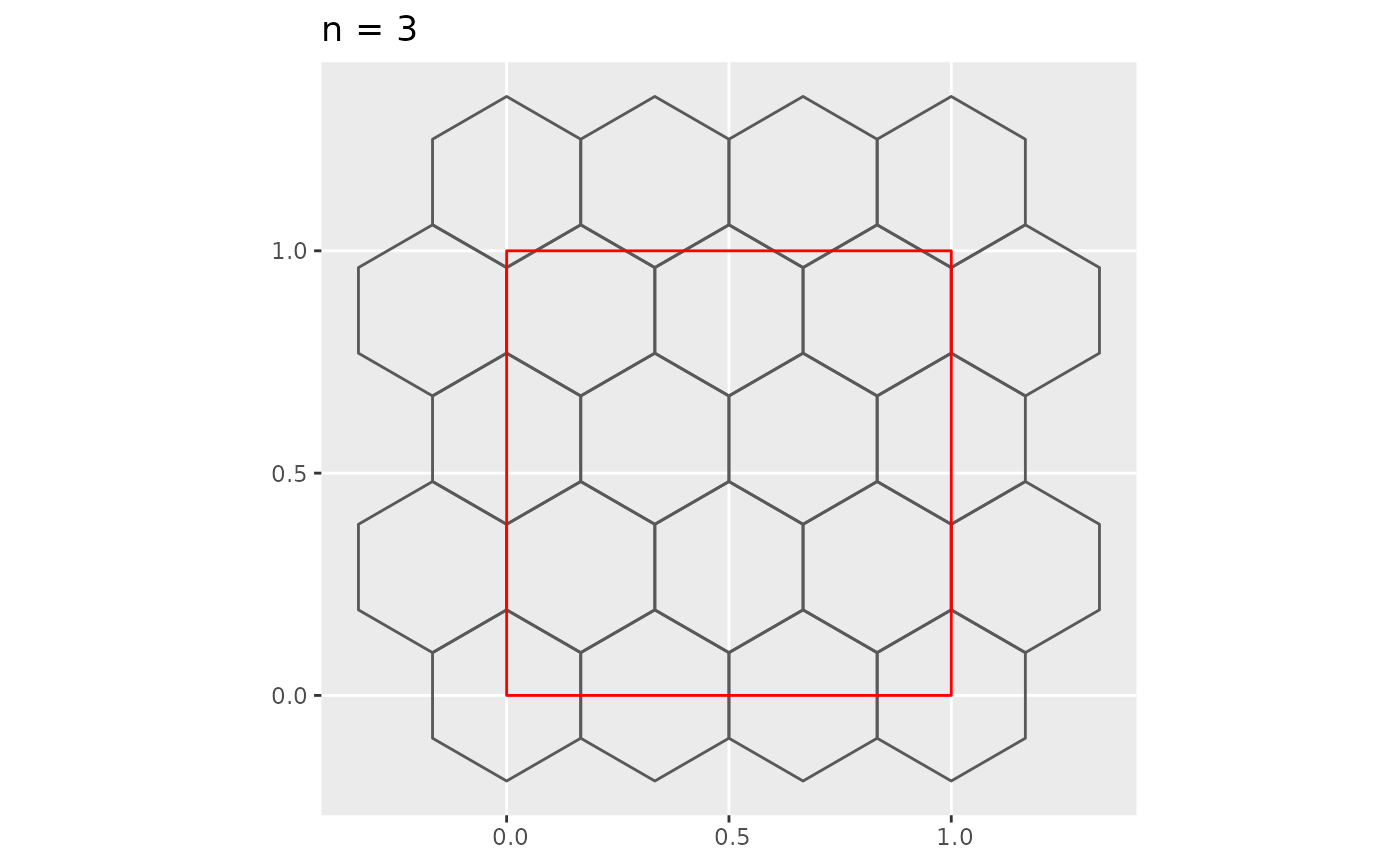

plot_hex_tile(n = 5)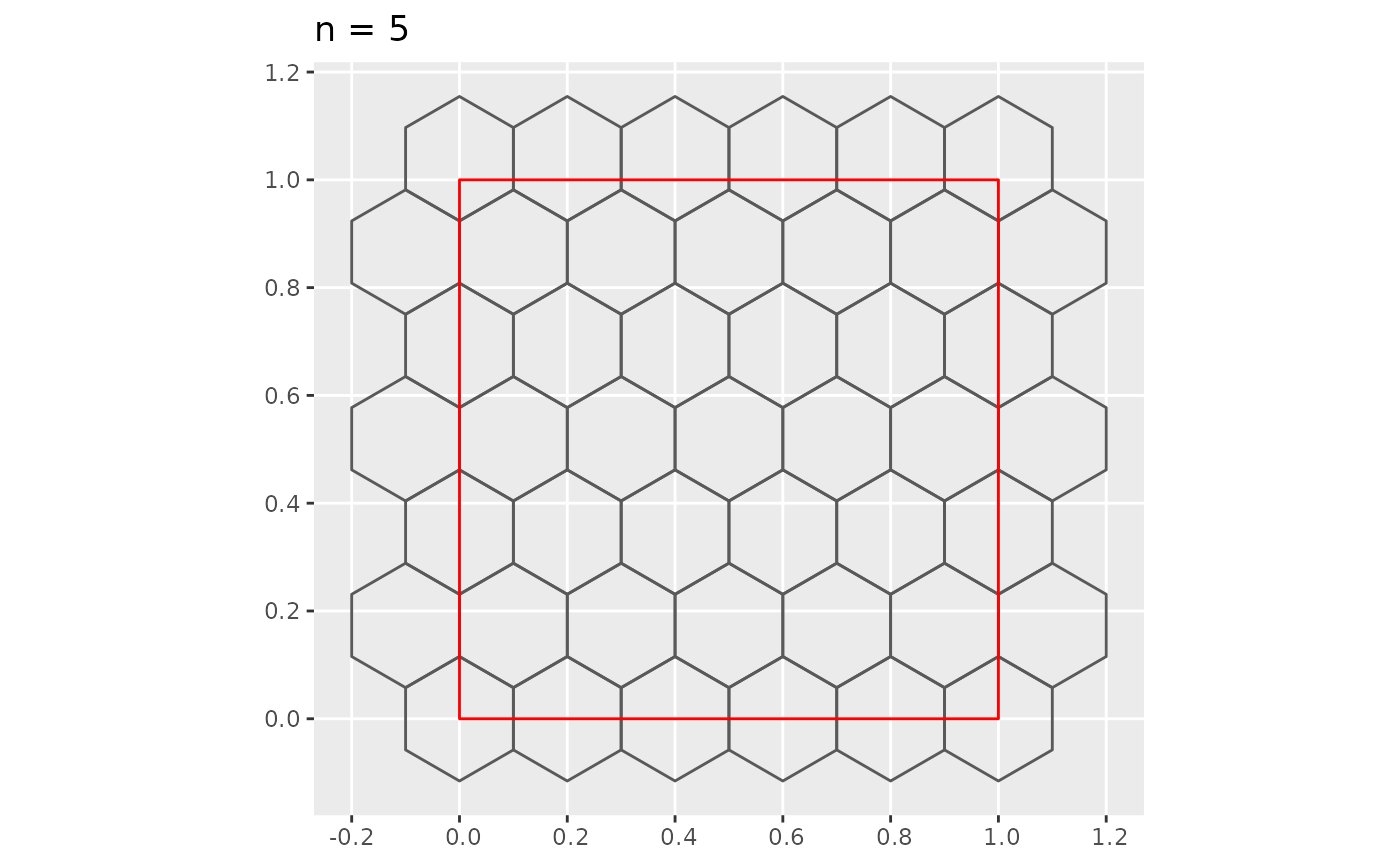

Using basic trigonometry for a regular hexagon of height $h$ , width $w$ and length $b$ as shown in the diagram below, you can find that $h = 2 w / \sqrt{3}$ and $b = w / \sqrt{3}$ .

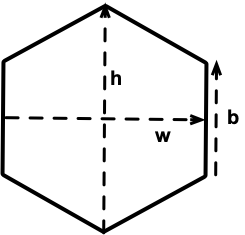
Putting it all together, you can find that the maximum and minimum number of hexagons in a row is $\lfloor x_2 - x_1 \rfloor / c + 2$ (even rows) and $\lfloor x_2 - x_1 \rfloor / c + 1$ (odd rows), respectively. The maximum and minimum number of hexagons in a column (which we define as the number of hexagon where its center passes through a vertical line) is $\lfloor (y_2 - y_1 + h / 2 - b) / (h + b) \rfloor + 1$ and $\lfloor (y_2 - y_1 + h / 2 - b) / (h + b) \rfloor$ (need to double check this).